Let α ∈ R be nonnegative and n ∈ N. Then there exists a unique non-negative x ∈ R such that x n = α.

 Existence of n-th roots of positive real numbers

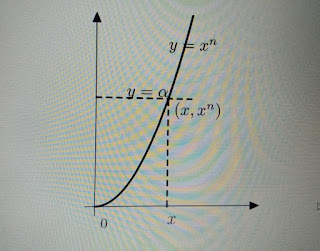
Strategy: Look at Figure 1.9. What we are looking for is the intersection of the graphs of the functions y = α and y = x n . The common point will have coordinates (x, xn ) and (x, α). Hence it will follow that x n = α.

Now how do we plan to get such an x? We work backward. Let b ≥ 0 be such that b n = α. Now b = lub [0, b) and any t ∈ [0, b) satisfies t n < α. Hence b may be thought of as the LUB of the set S := {t ≥ 0 : t n < α}. Now if S is non-empty and bounded above, let c := lub S. We hope to show that c n = α.

We show that c n < α or c n > α cannot happen. See Figure 1.10. If c n < α, the picture shows that we can find c1 > c, c1 very near to c, such that we still have c n 1 < α, c1 ∈ S. This shows that c1 ∈ S. Hence c1 ≤ c, a contradiction.

 

If c n > α,  we can find a c2 < c, c2 very near to c but we still have c n 2 > α. Since c2 < c, there exists t ∈ S such that t > c2 and hence t n > cn > α, a contradiction. Hence c n = α.

Now c1 > c and is very near to c and still retains c n 1 < α. How do we look for such c1? Naturally if k ∈ N is very large, we expect c1 = c + 1 k is very near to c and (c + 1 n ) n < α.

Similarly, for c2 we look for a k ∈ N such that (c − 1 k ) n > α.

In the first case, it behooves us to use the binomial expansion. We try to find an estimate of the form (c + 1/k) n ≤ c n + C k for some constant C. So, it suffices to make sure C/k < α − c n , possible by Archimedean property.

In the second case, we try to find an estimate of the form (c−1/k) n ≥ c n− C k . So, it suffices to make sure c n − C k > α. 

We claim that x n = α. Exactly one of the following is true: (i) x n < α, (ii) x n > α, or (iii) x n = α. We shall show that the first two possibilities do not arise. Case (i): Assume that x n < α. For any k ∈ N, we have (x + 1/k) n = x n + Xn j=1  n j  x n−j (1/kj ) ≤ x n + Xn j=1  n j  x n−j (1/k) = x n + C/k, where C := Xn j=1  n j  x n−j . If we choose k such that x n + C/k < α, that is, for k > C/(α − x n), it follows that (x + 1/k) n < α. Case (ii): Assume that x n > α. We have (−1)j (1/kj ) > −1/k for k ∈ N, j ≥ 1. We use this below. (x − 1/k) n = x n + Xn j=1  n j  (−1)jx n−j (1/kj ) ≥ x n − Xn j=1  n j  x n−j (1/k) = x n − C/k, where C := Xn j=1  n j  x n−j . If we choose k such that x n − C/k > α, that is, if we take k > C/(x n − α), it follows that (x − 1/k) n > α. We now show that if x and y are non-negative real numbers such that x n = y n = α, then x = y. Look at the following algebraic identity: (x n − y n ) ≡ (x − y) · [x n−1 + x n−2 y + · · · + xyn−2 + y n−1 ]. If x and y are nonnegative with x n = y n and if x 6= y, say, x > y, then the left-hand side is zero while both the factors in brackets on the right are strictly positive, a contradiction. 

This completes the proof of the theorem